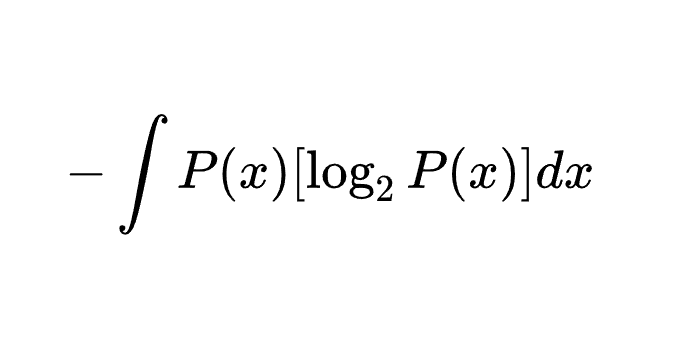熵

信息量

信息量是对信息的度量，我们接受到的信息量和具体发生的事情有关。

信息的大小和随机事件的概率负相关。概率越小的事情若发生了产生的信息量越大，因为它排除了别的很多的可能性，例如今天下冰雹；而概率越大的事情产生的信息量越小，例如太阳从东边升起并不会带来什么信息。

假设有不相关事件 $X$ 和 $Y$ ，若两个事件同时发生，其概率为 $P(X, Y)=P(X)*P(Y)$ ，产生的信息量为 $h(X, Y)=h(X)+h(Y)$ ，由此可见信息量 $h(X)$ 与发生概率 $P(X)$ 对数相关。

综上两条性质，可以定义信息量：

$h(X)=-\log_{2}P(X)$

底数为 2 这是因为只是遵循信息论的普遍传统，使用 2 作为对数的底。

熵（信息熵）

信息量度量的是一个具体事件发生了所带来的信息，而信息熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。熵简写为 $H$ ，定义为

$H(P)=Entropy=\mathbb{E}_{x\sim P}\left[-\log P(x)\right]$

对于离散随机变量 $X\sim P$ ，其公式为

$H(P)=-\sum_{i}P(x_{i})\log_{2}P(x_{i})$

对于连续随机变量 $X\sim P$ ，其公式为

$H(P)=-\int P(x)\left[\log_{2}P(x)\right]dx$

信息论中熵的概念首次被香农提出，目的是寻找一种高效/无损地编码信息的方法：以编码后数据的平均长度来衡量高效性，平均长度越小越高效；同时还需满足“无损”的条件，即编码后不能有原始信息的丢失。这样，香农提出了熵的理论定义：无损编码事件信息的最小平均编码长度。

对于最理想的情况， $N$ 个事件等可能，则每个事件编码长度为 $\log_{2} N=-\log\frac{1}{N}=-\log P$ ，那么平均最小编码长度就是 $-\sum_{i}P(i)\log P(i)$ 。这也是所有情况的平均编码长度的理论下限。

物理学中熵定义为 $S=k\ln\Omega$ 。

交叉熵

熵的估计

根据熵的公式定义可知，只要知道了任何事件的概率分布 $P$ ，就可以计算它的熵。然而，在不知道事件的概率分布的情况下，想要计算熵，只能去估计熵。

在观测之前，我们只有预估的概率分布 $Q$ ，使用估计得到的概率分布 $Q$ ，可以计算估计的熵：

$EstimatedEntropy=\mathbb{E}_{x\sim Q}\left[-\log Q(x)\right]$

交叉熵

然而，估计的概率分布 $Q$ 为公式引入了两部分的不确定性：不确定的概率分布 $Q$ 与不确定的最小编码长度 $-\log Q(x)$ ，因此估计的熵结果 $EstimatedEntropy$ 可能错得离谱，与真实的熵 $Entropy$ 对比毫无意义。

我们的目的是为了使估计的概率分布 $Q$ 尽可能接近真实的概率分布 $P$ ，也就是为了让平均最小编码长度尽可能小，而理论平均最小编码长度的值为熵 $Entropy=\mathbb{E}_{x\sim P}\left[-\log P(x)\right]$ ，因此我们需要对比最小编码长度 $-\log Q(x)$ 与 $-\log P(x)$ ，即通过 $\mathbb{E}_{x\sim P}\left[-\log Q(x)\right]$ 的值来评判 $Q$ 对 $P$ 的接近程度。

从而定义交叉熵：

$H(P,Q)=CrossEntropy=\mathbb{E}_{x\sim P}\left[-\log Q(x)\right]$

由交叉熵的定义可知，交叉熵的最小值为熵 $\mathbb{E}_{x\sim P}\left[-\log P(x)\right]$ ，当且仅当估计的概率分布 $Q$ 与真实的概率分布 $P$ 完全吻合时取得最小值。因此可以使用交叉熵作为损失函数，目标为最小化交叉熵。

为什么交叉熵用真实概率分布 $P$ 作为概率分布去计算估计的最小编码长度 $-\log Q(x)$ 的期望，而不是反过来，用估计的概率分布 $Q$ 作为概率分布去计算真实的最小编码长度 $-\log P(x)$ 的期望？

我们的目标是为了让 $Q$ 去回归 $P$ ，因此衡量标准必须以 $P$ 为基准，交叉熵表达的是在真实分布下，当前编码方案的平均编码长度；最小化交叉熵的过程意味着基于真实情况最优化编码方案。如果反过来定义，则没有意义；它优化的方向是未知的，甚至不能收敛，因为 $\mathbb{E}_{x\sim Q}\left[-\log P(x)\right]$ 未必一定大于 $\mathbb{E}_{x\sim P}\left[-\log P(x)\right]$ ，这是未知的。

交叉熵作为损失函数

假设一个动物照片的数据集中有 5 种动物，且每张照片中只有一只动物，每张照片的标签都是 one-hot 编码。

第一张照片是狗的概率为 100%，是其他的动物的概率是 0；第二张照片是狐狸的概率是 100%，是其他动物的概率是0；其余照片同理。因此可以计算下，每张照片的熵都为 0。换句话说，以 one-hot 编码作为标签的每张照片都有 100% 的确定度，不像别的描述概率的方式：狗的概率为 90%，猫的概率为 10%。

假设有两个机器学习模型对第一张照片分别作出了预测：Q1 和 Q2，而第一张照片的真实标签为 [1,0,0,0,0]。

两个模型预测效果如何呢，可以分别计算下交叉熵：

交叉熵对比了模型的预测结果和数据的真实标签，随着预测越来越准确，交叉熵的值越来越小，如果预测完全正确，交叉熵的值就为 0。因此，训练分类模型时，可以使用交叉熵作为损失函数。

KL 散度

KL 散度（相对熵）

假设有两个概率分布 $P$ 和 $Q$ ，且事件为连续型随机变量。对于单个事件 $x$ ，模型 $P$ 相对模型 $Q$ 的信息损失为信息量之差 $(-\log Q(x))-(-\log P(x))=\log(\frac{P(x)}{Q(x)})$ ；要衡量模型 $P$ 相对于模型 $Q$ 的整体损失（平均损失），需要计算所有事件的信息损失的平均，即为 $\int P(x)\log(\frac{P(x)}{Q(x)})dx$ 。

从而定义 $KL$ 散度：

$KL(P||Q)=\int P(x)\log(\frac{P(x)}{Q(x)})dx$

称作 $P$ 相对于 $Q$ 的 $KL$ 散度，其表达的含义为当我们认为（或假设）真实分布是 Q，但实际数据来自 P 时，所产生“信息损失”的平均值，一句话说就是用假设分布 $Q$ 去代表真实分布 $P$ 的代价。

从上述公式可以看出，当且仅当 $P=Q$ 时， $KL(P||Q)=0$ 。此外具有两个性质：非负性与不对称性。后者意味着 $P$ 对于 $Q$ 的 $KL$ 散度并不等于 $Q$ 对于 $P$ 的 $KL$ 散度。因此， $KL$ 散度并不是一个度量，即 $KL$ 散度并非距离。